Fourier Transform For Image Compression
Fourier Transformer for Image Compression
"One picture is equivalent of 1000 words"
As we all know in today's world data transfer ,sharing and storing is very important.Data is the new oil in 21st century for the small scale businesses and MNC's to run their businesses.The objective of image compression is to reduce irrelevance and redundancy of the image data to be able to store or transmit data in an efficient form. It is concerned with minimizing the number of bits required to represent an image. Image compression may be lossy or lossless
The Fourier Transform is an important image processing tool which is used to decompose an image into its sine and cosine components. The output of the transformation represents the image in the Fourier or frequency domain, while the input image is the spatial domain equivalent. In the Fourier domain image, each point represents a particular frequency contained in the spatial domain image.
The Fourier Transform is used in a wide range of applications, such as image analysis, image filtering, image reconstruction and image compression.
The areas where image compression is used are in television broadcasting, Remote sensing via satellite, for military communication systems through radars, Tele conferencing systems, communications systems built through computers, Facsimile transmission medical images in computer tomography magnetic resonance imaging.
How It Works
As we are only concerned with digital images, we will restrict this discussion to the Discrete Fourier Transform (DFT).
The DFT is the sampled Fourier Transform and therefore does not contain all frequencies forming an image, but only a set of samples which is large enough to fully describe the spatial domain image. The number of frequencies corresponds to the number of pixels in the spatial domain image, i.e. the image in the spatial and Fourier domain are of the same size.
For a square image of size N×N, the two-dimensional DFT is given by:
where f(a,b) is the image in the spatial domain and the exponential term is the basis function corresponding to each point F(k,l) in the Fourier space. The equation can be interpreted as: the value of each point F(k,l) is obtained by multiplying the spatial image with the corresponding base function and summing the result.
The basis functions are sine and cosine waves with increasing frequencies, i.e. F(0,0) represents the DC-component of the image which corresponds to the average brightness and F(N-1,N-1) represents the highest frequency.
In a similar way, the Fourier image can be re-transformed to the spatial domain. 
The inverse Fourier transform is given by:
Note the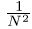 
normalization term in the inverse transformation. This normalization is sometimes applied to the forward transform instead of the inverse transform, but it should not be used for both.$$
To obtain the result for the above equations, a double sum has to be calculated for each image point. However, because the Fourier Transform is separable, it can be written as
where
Using these two formulas, the spatial domain image is first transformed into an intermediate image using N one-dimensional Fourier Transforms. This intermediate image is then transformed into the final image, again using N one-dimensional Fourier Transforms. Expressing the two-dimensional Fourier Transform in terms of a series of 2N one-dimensional transforms decreases the number of required computations.
Even with these computational savings, the ordinary one-dimensional DFT has 
complexity. This can be reduced to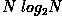 
if we employ the Fast Fourier Transform (FFT) to compute the one-dimensional DFTs. This is a significant improvement, in particular for large images. There are various forms of the FFT and most of them restrict the size of the input image that may be transformed, often to 
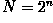where n is an integer. The mathematical details are well described in the literature.
The Fourier Transform produces a complex number valued output image which can be displayed with two images, either with the real and imaginary part or with magnitude and phase. In image processing, often only the magnitude of the Fourier Transform is displayed, as it contains most of the information of the geometric structure of the spatial domain image. However, if we want to re-transform the Fourier image into the correct spatial domain after some processing in the frequency domain, we must make sure to preserve both magnitude and phase of the Fourier image.
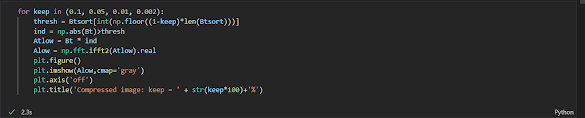
The Fourier domain image has a much greater range than the image in the spatial domain. Hence, to be sufficiently accurate, its values are usually calculated and stored in float values.
Here we are using keeep function to print different level of compression of images
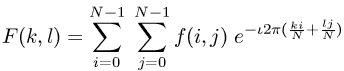
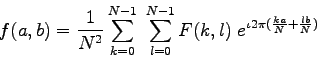
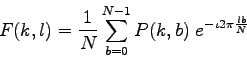
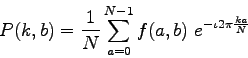
Comments
Post a Comment